電驢下載基地 >> 图书资源 >> 教育科技 >> 《黎曼幾何與幾何分析》(Riemannian Geometry and Geometric Analysis)(Jurgen Jost)4th[PDF]
| 《黎曼幾何與幾何分析》(Riemannian Geometry and Geometric Analysis)(Jurgen Jost)4th[PDF] | |
|---|---|
| 下載分級 | 图书资源 |
| 資源類別 | 教育科技 |
| 發布時間 | 2017/7/10 |
| 大 小 | - |
《黎曼幾何與幾何分析》(Riemannian Geometry and Geometric Analysis)(Jurgen Jost)4th[PDF] 簡介: 中文名 : 黎曼幾何與幾何分析 原名 : Riemannian Geometry and Geometric Analysis 別名 : Universitext 作者 : Jurgen Jost 資源格式 : PDF 版本 : 4th 出版社 : Springer 書號 : 3-540-42627-2 發行時間 : 2000年 地區 : 大陸,美國,英國,法國,德國
電驢資源下載/磁力鏈接資源下載:
全選
"《黎曼幾何與幾何分析》(Riemannian Geometry and Geometric Analysis)(Jurgen Jost)4th[PDF]"介紹
中文名: 黎曼幾何與幾何分析
原名: Riemannian Geometry and Geometric Analysis
別名: Universitext
作者: Jurgen Jost
資源格式: PDF
版本: 4th
出版社: Springer
書號: 3-540-42627-2
發行時間: 2000年
地區: 大陸,美國,英國,法國,德國
語言: 英文
簡介:

這本書我在我的另一個資源裡發過,現在單獨拿出來發一次。初學黎曼幾何的讀者可以去這裡看看:http://www.ed2000.com/ShowFile.asp?vid=2817268
這部書是Springer出版社Universitext系列的一本,過後我會整理UT的書發到VC上來。
這是一本關於黎曼幾何,尤其是幾何分析的優秀教材,但是書中關於純黎曼幾何的講述很簡潔,不太適合初學者,書中很大篇幅在講幾何分析的基本方法,適合對黎曼幾何已經有一定了解想從分析方面深入研究的讀者。
這是書中部分前言:
Riemannian geometry is characterized, and research is oriented towards and shaped by concepts (geodesics, connections, curvature, ...) and objectives, in particular to understand certain classes of (compact) Riemannian manifolds defined by curvature conditions (constant or positive or negative curvature, ...). By way of contrast, geometric analysis is a perhaps somewhat less systematic collection of techniques, for solving extremal problems naturally arising in geometry and for investigating and characterizing their solutions. It turns out that the two fields complement each other very well; geometric analysis offers tools for solving difficult problems in geometry, and Riemannian geometry stimulates progress in geometric analysis by setting ambitious goals.
It is the aim of this book to be a systematic and comprehensive introduction to Riemannian geometry and a representative introduction to the methods of geometric analysis. It attempts a synthesis of geometric and analytic methods in the study of Riemannian manifolds.
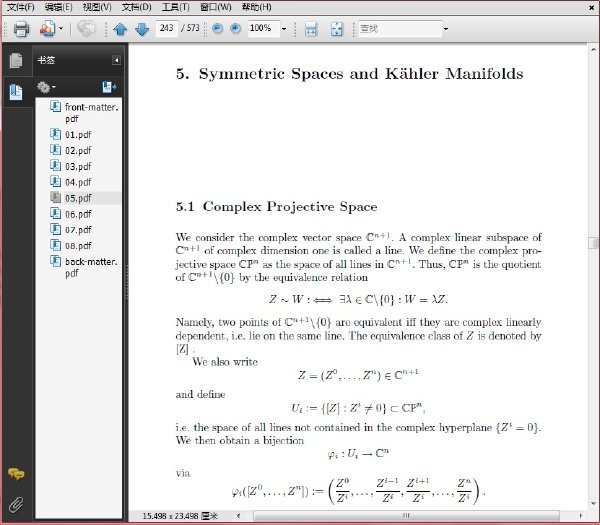
目錄:
1. Foundational Material
1.1 Manifolds and Differentiable Manifolds
1.2 Tangent Spaces
1.3 Submanifolds
1.4 Riemannian Metrics
1.5 Vector Bundles
1.6 Integral Curves of Vector Fields. Lie Algebras
1.7 Lie Groups
1.8 Spin Structures
Exercises for Chapter 1
2. De Rham Cohomology and Harmonic Differential Forms
2.1 The Laplace Operator
2.2 Representing Co homology Classes by Harmonic Forms
2.3 Generalizations
Exercises for Chapter 2
3. Parallel Transport, Connections, and Covariant Derivatives
3.1 Connections in Vector Bundles
3.2 Metric Connections. The Yang-Mills Functional
3.3 The Levi-Civita Connection
3.4 Connections for Spin Structures and the Dirac Operator ..
3.5 The Bochner Method
3.6 The Geometry of Submanifolds. Minimal Submanifolds ...
Exercises for Chapter 3
4. Geodesics and Jacobi Fields
4.1 1st and 2nd Variation of Arc Length and Energy
4.2 Jacobi Fields
4.3 Conjugate Points and Distance Minimizing Geodesics ...
4.4 Riemannian Manifolds of Constant Curvature
4.5 The Rauch Comparison Theorems and Other Jacobi Field Estimates
4.6 Geometric Applications of Jacobi Field Estimates
4.7 Approximate Fundamental Solutions and Representation Formulae
4.8 The Geometry of Manifolds of Nonpositive Sectional Curvature
Exercises for Chapter 4
A Short Survey on Curvature and Topology
5. Symmetric Spaces and Kahler Manifolds
5.1 Complex Projective Space
5.2 Kahler Manifolds
5.3 The Geometry of Symmetric Spaces
5.4 Some Results about the Structure of Symmetric Spaces ..
5.5 The Space SI(n,R)/SO(n,R)
5.6 Symmetric Spaces of Noncompact Type as Examples of Nonpositively Curved Riemannian Manifolds
Exercises for Chapter 5
6. Morse Theory and Floer Homology
6.1 Preliminaries: Aims of Morse Theory
6.2 Compactness: The Palais-Smale Condition and the Existence of Saddle Points
6.3 Local Analysis: Nondegeneracy of Critical Points, Morse Lemma, Stable and Unstable Manifolds
6.4 Limits of Trajectories of the Gradient Flow
6.5 The Morse-Smale-Floer Condition: Transversality and Z2-Cohomology
6.6 Orientations and Z-homology
6.7 Homotopies
6.8 Graph flows
6.9 Orientations
6.10 The Morse Inequalities
6.11 The Palais-Smale Condition and the Existence of Closed Geodesics
Exercises for Chapter 6
7. Variational Problems from Quantum Field Theory ..
7.1 The Ginzburg-Landau Functional
7.2 The Seiberg-Witten Functional
Exercises for Chapter 7
8. Harmonic Maps
Appendix
Bibliography
Index
原名: Riemannian Geometry and Geometric Analysis
別名: Universitext
作者: Jurgen Jost
資源格式: PDF
版本: 4th
出版社: Springer
書號: 3-540-42627-2
發行時間: 2000年
地區: 大陸,美國,英國,法國,德國
語言: 英文
簡介:

這本書我在我的另一個資源裡發過,現在單獨拿出來發一次。初學黎曼幾何的讀者可以去這裡看看:http://www.ed2000.com/ShowFile.asp?vid=2817268
這部書是Springer出版社Universitext系列的一本,過後我會整理UT的書發到VC上來。
這是一本關於黎曼幾何,尤其是幾何分析的優秀教材,但是書中關於純黎曼幾何的講述很簡潔,不太適合初學者,書中很大篇幅在講幾何分析的基本方法,適合對黎曼幾何已經有一定了解想從分析方面深入研究的讀者。
這是書中部分前言:
Riemannian geometry is characterized, and research is oriented towards and shaped by concepts (geodesics, connections, curvature, ...) and objectives, in particular to understand certain classes of (compact) Riemannian manifolds defined by curvature conditions (constant or positive or negative curvature, ...). By way of contrast, geometric analysis is a perhaps somewhat less systematic collection of techniques, for solving extremal problems naturally arising in geometry and for investigating and characterizing their solutions. It turns out that the two fields complement each other very well; geometric analysis offers tools for solving difficult problems in geometry, and Riemannian geometry stimulates progress in geometric analysis by setting ambitious goals.
It is the aim of this book to be a systematic and comprehensive introduction to Riemannian geometry and a representative introduction to the methods of geometric analysis. It attempts a synthesis of geometric and analytic methods in the study of Riemannian manifolds.

目錄:
1. Foundational Material
1.1 Manifolds and Differentiable Manifolds
1.2 Tangent Spaces
1.3 Submanifolds
1.4 Riemannian Metrics
1.5 Vector Bundles
1.6 Integral Curves of Vector Fields. Lie Algebras
1.7 Lie Groups
1.8 Spin Structures
Exercises for Chapter 1
2. De Rham Cohomology and Harmonic Differential Forms
2.1 The Laplace Operator
2.2 Representing Co homology Classes by Harmonic Forms
2.3 Generalizations
Exercises for Chapter 2
3. Parallel Transport, Connections, and Covariant Derivatives
3.1 Connections in Vector Bundles
3.2 Metric Connections. The Yang-Mills Functional
3.3 The Levi-Civita Connection
3.4 Connections for Spin Structures and the Dirac Operator ..
3.5 The Bochner Method
3.6 The Geometry of Submanifolds. Minimal Submanifolds ...
Exercises for Chapter 3
4. Geodesics and Jacobi Fields
4.1 1st and 2nd Variation of Arc Length and Energy
4.2 Jacobi Fields
4.3 Conjugate Points and Distance Minimizing Geodesics ...
4.4 Riemannian Manifolds of Constant Curvature
4.5 The Rauch Comparison Theorems and Other Jacobi Field Estimates
4.6 Geometric Applications of Jacobi Field Estimates
4.7 Approximate Fundamental Solutions and Representation Formulae
4.8 The Geometry of Manifolds of Nonpositive Sectional Curvature
Exercises for Chapter 4
A Short Survey on Curvature and Topology
5. Symmetric Spaces and Kahler Manifolds
5.1 Complex Projective Space
5.2 Kahler Manifolds
5.3 The Geometry of Symmetric Spaces
5.4 Some Results about the Structure of Symmetric Spaces ..
5.5 The Space SI(n,R)/SO(n,R)
5.6 Symmetric Spaces of Noncompact Type as Examples of Nonpositively Curved Riemannian Manifolds
Exercises for Chapter 5
6. Morse Theory and Floer Homology
6.1 Preliminaries: Aims of Morse Theory
6.2 Compactness: The Palais-Smale Condition and the Existence of Saddle Points
6.3 Local Analysis: Nondegeneracy of Critical Points, Morse Lemma, Stable and Unstable Manifolds
6.4 Limits of Trajectories of the Gradient Flow
6.5 The Morse-Smale-Floer Condition: Transversality and Z2-Cohomology
6.6 Orientations and Z-homology
6.7 Homotopies
6.8 Graph flows
6.9 Orientations
6.10 The Morse Inequalities
6.11 The Palais-Smale Condition and the Existence of Closed Geodesics
Exercises for Chapter 6
7. Variational Problems from Quantum Field Theory ..
7.1 The Ginzburg-Landau Functional
7.2 The Seiberg-Witten Functional
Exercises for Chapter 7
8. Harmonic Maps
Appendix
Bibliography
Index
- 上一頁:《黎曼幾何相關教材》(Riemannian Geometry)(Jurgen Jost & Peter Petersen & 伍鴻熙等)[DJVU]
- 下一頁:《相圖原理和冶金相圖》(陳國發 & 李運剛)掃描版[PDF]
相關資源:
- [文學圖書]《頑主》(王朔)文字版[PDF]
- [人文社科]《心理學其實很好玩》掃描版[PDF]
- [教育科技]《二階拋物型偏微分方程》掃描版[DJVU]
- [文學圖書]《走在鄉土上:歷史人類學札記》(王銘銘)掃描版[PDF]
- [生活圖書]《人生的鑰匙:如何培養孩子的自尊心》掃描版[PDF]
- [人文社科]《和大衛哈維一起讀資本論》(Reading Marx’s Capital with David Harvey)
- [經濟管理]《公司的力量 決戰華爾街》掃描版[PDF]
- [文學圖書]《兔子回家》((美)厄普代克)掃描版[PDF]
- [文學圖書]《魯迅經典全集》文字版[EPUB]
- [生活圖書]《外科疾病外治法》掃描版[PDF]
- [其他資源綜合]《股票培訓課程--殷保華講座》[壓縮包]
- [生活圖書]《孩子情緒異常的診療與預防》掃描版[PDF]
- [其他圖書]《標准類資料(個人收集的)》
- [其他圖書]《人類學與現代生活》((美)博厄斯)掃描版[PDF]
- [光盤游戲]《迷失危城》(Lost In The City)[光盤鏡像]
- [經濟管理]《借東風 職場資源“借力”大絕招》掃描版[PDF]
- [人文社科]《3D Total 網站CG作品收集》(3D Total)[壓縮包]
- [計算機與網絡]《PowerBuilder10 編程技術全接觸》掃描版[PDF]
- [其他資源綜合]《法國帝國時期軍服》(Uniforms Of the Armies Of France 1690-1894) 資料下載
- [硬盤游戲]《魔幻卡牌》(Spectromancer)漢化版[壓縮包]
- 中國性科學百科全書 PDF 高清掃描版版(128M)
- 《實用大學英語語法》掃描版[PDF]
- 《3D MAX 室內燈光教程》(3DTotal Lighting La Salle
- 《消化外科學》(皮執民)掃描版[PDF]
- 《大學生創業實踐》掃描版[PDF]
- 《現代空戰》(MODERN AIR COMBAT (By Fox2000))(Fox2000)[P
- 《洞察危機的驚魂:應激心理學》掃描版[PDF]
- 《油田原油含水測量》文字版[PDF]
- 《市政公用工程管理與實務(附贈光盤1張)(全國二
- 《水產基因組技術與研究進展》掃描版[PDF]
- 《自適應內模控制》(Adaptive Internal Model Control)文字版[PDF]
- 《輕松聽懂CNN新聞英語 中級》掃描版[PDF]
免責聲明:本網站內容收集於互聯網,本站不承擔任何由於內容的合法性及健康性所引起的爭議和法律責任。如果侵犯了你的權益,請通知我們,我們會及時刪除相關內容,謝謝合作! 聯系信箱:[email protected]
Copyright © 電驢下載基地 All Rights Reserved



